Education
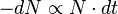
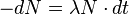
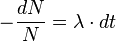
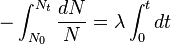
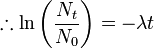
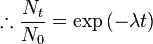
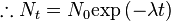
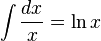
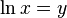
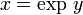
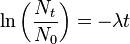
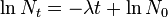
- How Black Holes Tick?
Black holes are incredibly massive, but cover only a small region. Because of the relationship between mass and gravity, this means they have an extremely powerful gravitational force. Virtually nothing can escape from them — under classical...
- Difference Between Atom Bomb And Hydrogen Bomb
The atom bomb The A-bomb, short for atom or atomic bomb, uses fission, which basically means splitting. Neutrons released during the process cause a chain reaction, causing fission in more and more cells. In uranium and plutonium, the elements used in...
- Marie Curie’s Research Papers Are Still Radioactive 100+ Years Later
When researching a famous historical figure, access to their work and materials usually proves to be one of the biggest obstacles. But things are much more difficult for those writing about the life of Marie Curie, the scientist who, along her with...
- Laplace's Correction To Newton's Formula
Assuming isothermal conditions to prevail when sound travels through air, Newton has applied Boyle's law to the changes in pressure and volume. In a region of compression, there is a slight increase in temperature and in a region of rarefaction, there...
- Half Life Of Radio Active Decay
Most of us have not been taught to think instinctively in terms of logarithmic or exponential terms even though many natural phenomena display exponential behaviours. Most of the forms of thinking which we have been taught in school are based on linear...
Education
Laws Of Radioactive Decay
The Radioactive Decay Law
Let us now use some symbols to reduce the amount of writing we have to do to describe what is going on and to avail ourselves of some mathematical techniques to simplify the situation even further than we have been able to do so far.
Let us say that in the sample of radioactive material there are N nuclei which have not decayed at a certain time, t. So what happens in the next brief period of time? Some nuclei will decay for sure. But how many?
On the basis of our reasoning above we can say that the number which will decay will depend on overall number of nuclei, N, and also on the length of the brief period of time. In other words the more nuclei there are the more will decay and the longer the time period the more nuclei will decay. Let us denote the number which will have decayed as dN and the small time interval as dt.
So we have reasoned that the number of radioactive nuclei which will decay during the time interval from t to t+dt must be proportional to N and to dt. In symbols therefore:
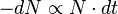
the minus sign indicating that N is decreasing.
Turning the proportionality in this equation into an equality we can write:
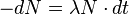
where the constant of proportionality, λ, is called the Decay Constant.
Dividing across by N we can rewrite this equation as:
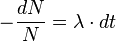
So this equation describes the situation for any brief time interval, dt. To find out what happens for all periods of time we simply add up what happens in each brief time interval. In other words we integrate the above equation. Expressing this more formally we can say that for the period of time from t = 0 to any later time t, the number of radioactive nuclei will decrease from N0 to Nt, so that:
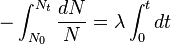
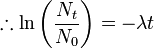
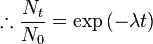
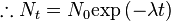
This final expression is known as the Radioactive Decay Law. It tells us that the number of radioactive nuclei will decrease in an exponential fashion with time with the rate of decrease being controlled by the Decay Constant.
Before looking at this expression in further detail let us review the mathematics which we used above. First of all we used integral calculus to figure out what was happening over a period of time by integrating what we knew would occur in a brief interval of time. Secondly we used a calculus relationship that the
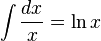
where ln x represents the natural logarithm of x. And thirdly we used the definition of logarithms that when
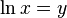
then,
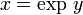
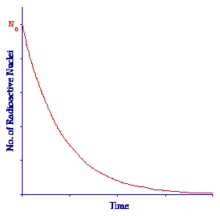
Now, to return to the Radioactive Decay Law. The Law tells us that the number of radioactive nuclei will decrease with time in an exponential fashion with the rate of decrease being controlled by the Decay Constant. The Law is shown in graphical form in the figure below:

The graph plots the number of radioactive nuclei at any time, Nt, against time, t. We can see that the number of radioactive nuclei decreases from N0 that is the number at t = 0 in a rapid fashion initially and then more slowly in the classic exponential manner.
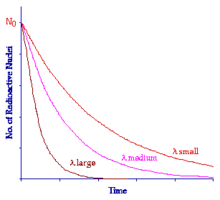
The influence of the Decay Constant can be seen in the following figure:

All three curves here are exponential in nature, only the Decay Constant is different. Notice that when the Decay Constant has a low value the curve decreases relatively slowly and when the Decay Constant is large the curve decreases very quickly.
The Decay Constant is characteristic of individual radionuclides. Some like uranium-238 have a small value and the material therefore decays quite slowly over a long period of time. Other nuclei such as technetium-99m have a relatively large Decay Constant and they decay far more quickly.
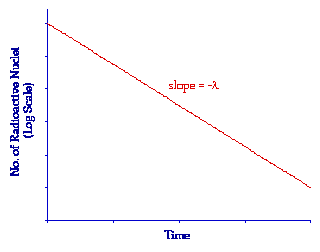
It is also possible to consider the Radioactive Decay Law from another perspective by plotting the logarithm of Nt against time. In other words from our analysis above by plotting the expression:
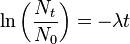
in the form
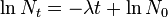
Notice that this expression is simply an equation of the form y = mx + c where m = -l and c = ln N0. As a result it is the equation of a straight line of slope -l as shown in the following figure. Such a plot is sometimes useful when we wish to consider a situation without the complication of the direct exponential behaviour.

For Half Life; Click Here
- How Black Holes Tick?
Black holes are incredibly massive, but cover only a small region. Because of the relationship between mass and gravity, this means they have an extremely powerful gravitational force. Virtually nothing can escape from them — under classical...
- Difference Between Atom Bomb And Hydrogen Bomb
The atom bomb The A-bomb, short for atom or atomic bomb, uses fission, which basically means splitting. Neutrons released during the process cause a chain reaction, causing fission in more and more cells. In uranium and plutonium, the elements used in...
- Marie Curie’s Research Papers Are Still Radioactive 100+ Years Later
When researching a famous historical figure, access to their work and materials usually proves to be one of the biggest obstacles. But things are much more difficult for those writing about the life of Marie Curie, the scientist who, along her with...
- Laplace's Correction To Newton's Formula
Assuming isothermal conditions to prevail when sound travels through air, Newton has applied Boyle's law to the changes in pressure and volume. In a region of compression, there is a slight increase in temperature and in a region of rarefaction, there...
- Half Life Of Radio Active Decay
Most of us have not been taught to think instinctively in terms of logarithmic or exponential terms even though many natural phenomena display exponential behaviours. Most of the forms of thinking which we have been taught in school are based on linear...
